Leonardo da Vinci’nin Çekme Testi

Kırılmanın istatistiksel doğası üzerine 500 yıllık bir deney.

Leonardo da Vinci’nin defterlerinde, 500 yıl önce gerçekleştirilmiş, demir kabloların (tellerin) eksenel dayanımının belirlenmesi üzerine “Farklı uzunluktaki demir tellerin dayanımının test edilmesi” isimli bir deney mevcut. Kendi ifadesiyle [1]:

Bu deneyin amacı, bir demir telin yük taşıma kapasitesini tayin etmektir. Yaklaşık 1,3 metre (2 braccia) uzunluğundaki bir demir tel, rijit bir mesnete sabitlenir; ardından telin ucuna bir sepet veya benzeri bir yük haznesi asılır ve bir besleme hunisinin ucundaki küçük delikten hazneye ince kum aktarılır. Telde kopma gerçekleştiği anda deliği kapatarak akışı kesecek yaylı bir mekanizma sisteme entegre edilmiştir. Düşme mesafesi çok kısa olduğundan, düşüş esnasında haznenin stabilitesi bozulmaz (devrilmez). Biriken kumun ağırlığı (kopma yükü) ve tel üzerindeki kopma kesitinin konumu kaydedilir. Sonuçların doğrulanması amacıyla deney birkaç kez tekrarlanır. Müteakiben, tel uzunluğu yarıya indirilerek (önceki boyun 1/2’si) test edilir ve taşıdığı ilave yük kaydedilir; daha sonra uzunluk dörtte bire (1/4) düşürülür ve süreç bu şekilde devam ettirilir. Her aşamada nihai mukavemet değeri ve kopma lokasyonu not edilir.

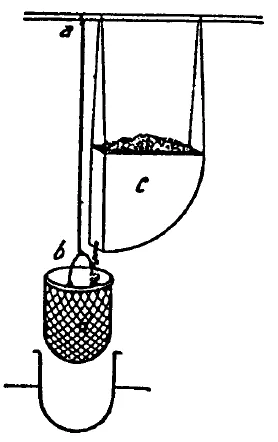
Kablo uzunluğu kısaldıkça dayanımın artması mevcut temel mukavemet bilgimiz ışığında bize anlamsız görünür. Ne de olsa:

Teli koparacak eksenel yük telin uzunluğuna değil kesit alanına bağlıdır. Acaba da Vinci terim seçiminde hata yapıp telin çapı yerine yanlışlıkla uzunluğu mu demiştir [2]? Durum tam olarak böyle değil. Dikkat edilirse da Vinci sonuçların doğrulanması amacıyla her bir testin birkaç kez tekrarlanmasından bahsediyor. Çünkü malzeme özellikleri:

• Ölçümden kaynaklı hatalar
• Malzemeden kaynaklı sebepler

Nedeniyle istatistiksel olarak varyasyon gösterirler. Malzemeden kaynaklı sebepleri (kusurlar) göz önünde bulunduralım: Eğer uzun bir teli, $L_0$ birim tel uzunluğu olmak üzere $x$ adet birim uzunlukta telin birbirine eklenmesi olarak düşünürsek telin yüke dayanma olasılığı:

olarak ifade edilir. Dikkat edilirse yazı tura atmaya benzer bir durum mevcuttur. Tek seferde yazı ya da tura atma ihtimali $1/2$ iken birden fazla kere üst üste yazı ya da tura ihtimali her atışta azalmaktadır. Aynı şekilde burada da kablomuzu birim uzunluktaki kablolardan müteşekkil düşünürsek, her bir birim kablo eklendiğinde telin yüke dayanma olasılığı da azalmaktadır. Bunun sebebi ise uzunluğun artışı ile birlikte malzeme kusurlarının artışıdır. Aynı şey (aynı dayanma olasılığı için) hacimler için de geçerlidir [3]. Leonardo da Vinci 500 sene öncesinden bizlere kırılma mekaniği dersi veriyor.

Kaynaklar

[1] Parsons, W. B. (1968). Engineers and Engineering in the Renaissance.
[2] Lund, J. R., & Byrne, J. P. (2001). Leonardo da Vinci’s tensile strength tests: implications for the discovery of engineering mechanics. Civil engineering systems, 18(3), 243-250.
[3] Hertzberg, R. W., Vinci, R. P., & Hertzberg, J. L. (2020). Deformation and fracture mechanics of engineering materials. John Wiley & Sons.